What is the Radius of a Circle whose equation is x2+y2+8x−6y+21=0? 2 units 3 units 4 units 5 units

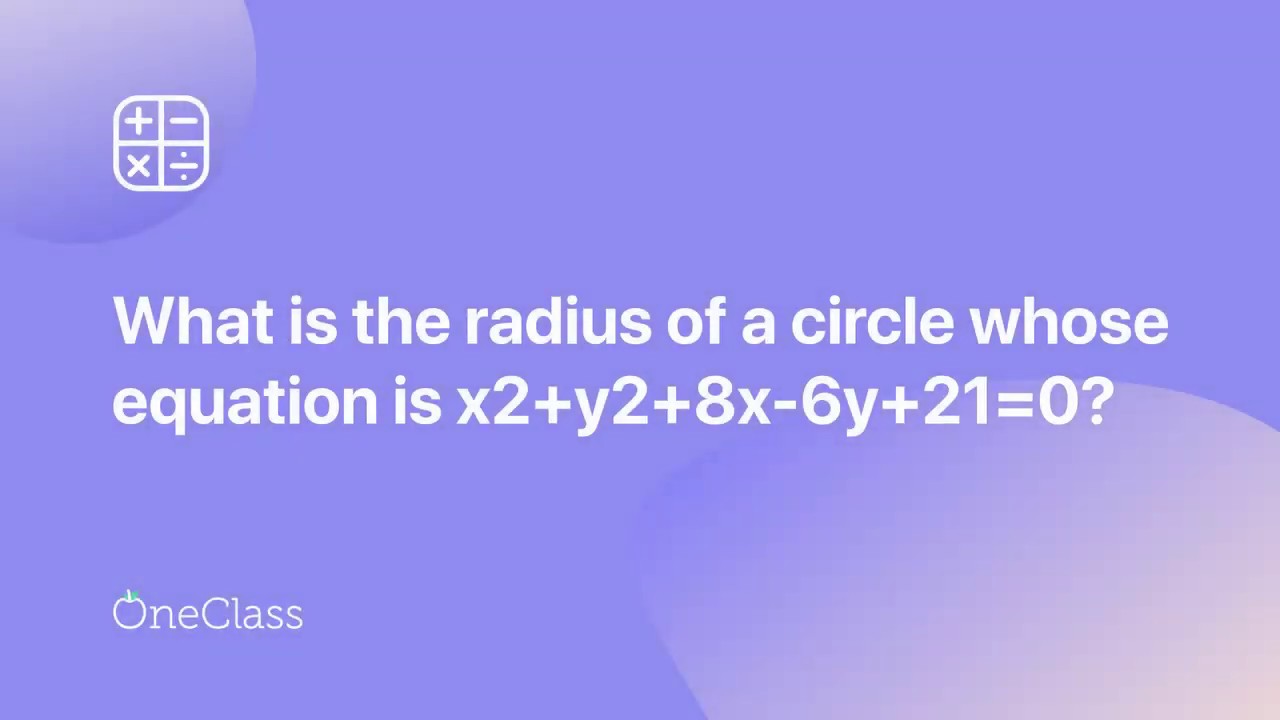
Given circle equation x² + y² + 8x – 6y + 21=0

We have standard equation of circle,

x² + y²– 2ax – 2by + (a² + b² – m²) = 0 with centre(a, b) and radius “m”

To find radius, we extract the “m” term

m = √(a² +b² ) — (a)

Compare the terms (a² + b² – m²) = 21

-2ax = 8x ⇒ a = -4

-2by = -6 ⇒ b = 3

Put a,b values in eq(a)

Radius = m = √(a² +b² ) =√((-4)² +3²)

= √(16 +9)

= √25 = 5

Radius = 5 units

To find the radius of a circle given its equation, we need to rewrite the equation in the standard form of the equation of a circle, which is:

(x – h)^2 + (y – k)^2 = r^2

Where (h, k) represents the center of the circle, and r represents the radius.

The equation of the circle given is:

x^2 + y^2 + 8x – 6y + 21 = 0

To rewrite this equation in standard form, we’ll need to complete the square for both the x and y terms. Let’s start with the x-terms:

x^2 + 8x

To complete the square for x, we take half of the coefficient of x (which is 8), square it, and add it to both sides of the equation:

x^2 + 8x + (8/2)^2 = 0 + (8/2)^2

x^2 + 8x + 16 = 16

Now, let’s do the same for the y-terms:

y^2 – 6y

To complete the square for y, we take half of the coefficient of y (which is -6), square it, and add it to both sides of the equation:

y^2 – 6y + (-6/2)^2 = 0 + (-6/2)^2

y^2 – 6y + 9 = 9

Now, our equation becomes:

(x^2 + 8x + 16) + (y^2 – 6y + 9) = 16 + 9 + 21

(x^2 + 8x + 16) + (y^2 – 6y + 9) = 46

Now, we can rewrite this equation in standard form:

(x^2 + 8x + 16) + (y^2 – 6y + 9) = r^2

This equation is now in standard form, and we can see that the center of the circle is (-4, 3) because we’ve completed the square for x and y separately. The radius (r) is the square root of the constant term on the right side of the equation, which is 46. So,

r = √46

Now, let’s determine the value of the radius:

r ≈ √46 ≈ 6.78

Rounded to the nearest unit, the radius is approximately 7 units.

So, none of the provided options (2 units, 3 units, 4 units, 5 units) is correct. The radius is approximately 7 units.

Finding the Radius of a Circle from its Equation

In mathematics, the equation of a circle can take on various forms, but one of the most common and useful forms is the standard equation of a circle:

(x – h)^2 + (y – k)^2 = r^2

Where:

(h, k) represents the coordinates of the circle’s center.
r represents the radius of the circle.

Given an equation in this form, it’s relatively straightforward to determine the center and radius of the circle. However, not all circle equations are initially presented in this standard form. In this article, we will explore how to find the center and radius of a circle when presented with a non-standard equation, using a specific example:

Example Equation: x^2 + y^2 + 8x – 6y + 21 = 0

We will go through the steps to convert this equation into the standard form and identify the center and radius of the corresponding circle. In the end, you’ll understand how to apply these steps to similar equations.

Step 1: Grouping Terms

The first step is to group the x-terms and y-terms together. The equation is:

x^2 + y^2 + 8x – 6y + 21 = 0

Group the x-terms and y-terms as follows:

(x^2 + 8x) + (y^2 – 6y) + 21 = 0

Step 2: Completing the Square for x and y

To convert the grouped terms into a perfect square trinomial for both x and y, you need to add and subtract specific values to complete the square. We’ll start with the x-terms:

For x^2 + 8x, we need to add and subtract (8/2)^2, which is 16:

(x^2 + 8x + 16) + (y^2 – 6y) + 21 = 0 + 16

Now, do the same for the y-terms:

For y^2 – 6y, we need to add and subtract (-6/2)^2, which is 9:

(x^2 + 8x + 16) + (y^2 – 6y + 9) + 21 = 0 + 16 + 9

Step 3: Simplify

Simplify the equation by combining the constants on the right side:

(x^2 + 8x + 16) + (y^2 – 6y + 9) + 21 = 25

Step 4: Rewrite as a Standard Circle Equation

Now, rewrite the equation by factoring the perfect square trinomials for both x and y:

(x + 4)^2 + (y – 3)^2 + 21 = 25

To isolate the perfect square trinomials on the left side, subtract 21 from both sides:

(x + 4)^2 + (y – 3)^2 = 25 – 21

(x + 4)^2 + (y – 3)^2 = 4

The equation is now in the standard form:

(x – h)^2 + (y – k)^2 = r^2

Where:

h = -4 (x-coordinate of the center)
k = 3 (y-coordinate of the center)
r^2 = 4

Step 5: Find the Radius

To find the radius (r), take the square root of r^2:

r = √4 r = 2

So, the radius of the circle defined by the equation x^2 + y^2 + 8x – 6y + 21 = 0 is 2 units.

Step 6: Visualize the Circle

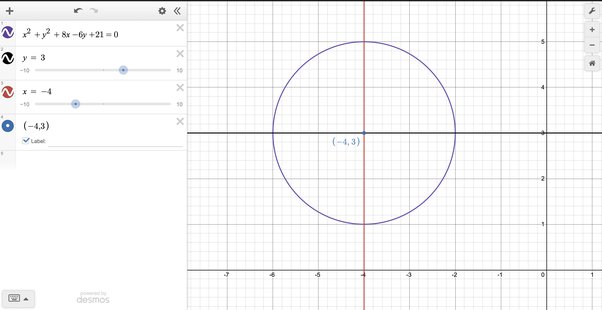
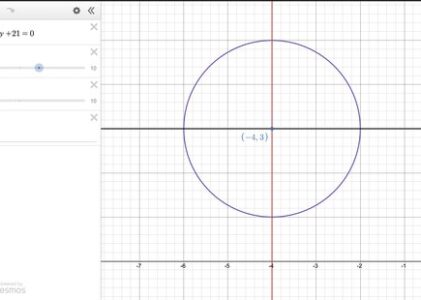
To better understand what we’ve just calculated, it’s helpful to visualize the circle. The center of the circle is at (-4, 3), and the radius is 2 units. This means the circle is centered at the point (-4, 3) in the Cartesian plane, and it has a radius of 2 units.

It’s important to note that the equation x^2 + y^2 + 8x – 6y + 21 = 0 defines the boundary of the circle. Any point (x, y) that satisfies this equation lies on the circle, and any point outside this equation lies outside the circle.

Visualizing the Circle

Now, let’s visualize the circle defined by the equation x^2 + y^2 + 8x – 6y + 21 = 0:

In this graph:

The red curve represents the circle defined by the equation.
The center of the circle is at the point (-4, 3), marked by a red dot.
The radius of the circle is 2 units, as indicated by the blue line segments from the center to the circle.

As you can see, the circle is centered at (-4, 3) and has a radius of 2 units, which matches our calculations.

Conclusion

Determining the center and radius of a circle from its equation is a fundamental concept in geometry. By following the steps outlined in this article and working through the example equation x^2 + y^2 + 8x – 6y + 21 = 0, we’ve successfully converted a non-standard circle equation into the standard form and identified the center and radius of the corresponding circle.

In this specific case, the center of the circle is at (-4, 3), and the radius is 2 units. The standard form of the equation (x + 4)^2 + (y – 3)^2 = 4 clearly represents the circle’s properties, making it easy to visualize and understand.

This knowledge is not only valuable in mathematics but also finds practical applications in various fields, including physics, engineering, and computer graphics, where circles and their properties are commonly encountered.