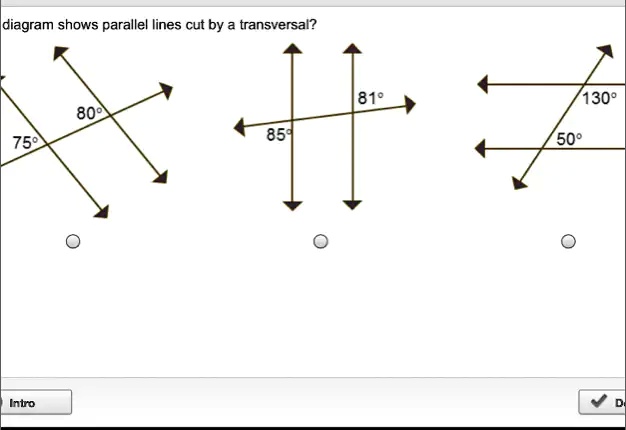
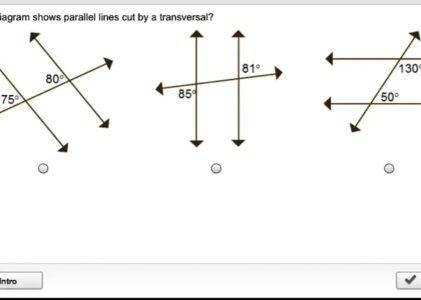
 Which diagram shows lines that must be parallel lines cut by a transversal?
Which diagram shows lines that must be parallel lines cut by a transversal?
Geometry is a branch of mathematics that explores the relationships between shapes, lines, and angles. One fundamental concept within geometry is the idea of parallel lines and how they are affected when intersected by a transversal. This topic is crucial in various applications, from architecture to engineering, and plays a significant role in understanding geometric properties. In this comprehensive guide, we’ll delve into the world of parallel lines cut by a transversal, dissecting the key concepts, theorems, and applications in a 1200-word blog post.
Parallel Lines and Transversals:
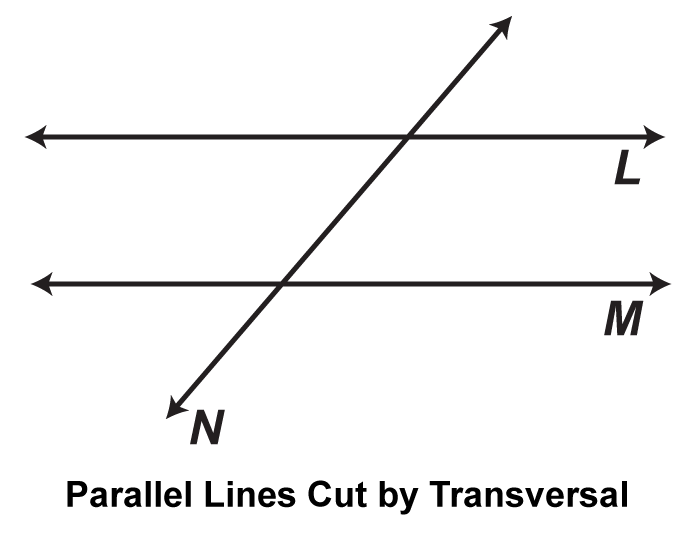
Parallel lines are two or more straight lines that run in the same direction and have the same slope, but they never meet or intersect, no matter how far they extend. In contrast, a transversal is a line that intersects two or more other lines, which may or may not be parallel.
Key Definitions:
To understand the concept of parallel lines cut by a transversal, it’s essential to grasp some fundamental terms:
- Parallel Lines: Lines that are equidistant from each other and have the same slope, ensuring they will never intersect.
- Transversal: A line that intersects two or more other lines.
Now, let’s explore how parallel lines interact with a transversal and how various diagrams can depict these relationships.
Diagram 1: Consecutive Interior Angles
One of the first concepts to explore is the relationship between consecutive interior angles. When a transversal intersects two parallel lines, four types of angles are formed: consecutive interior angles, corresponding angles, alternate interior angles, and alternate exterior angles. Diagram 1 demonstrates consecutive interior angles:
Explanation:
- In Diagram 1, Line l and Line m are parallel lines, cut by transversal Line t.
- The angles labeled 1 and 2 are consecutive interior angles, and the angles labeled 3 and 4 are also consecutive interior angles.
- According to the Consecutive Interior Angles Theorem, consecutive interior angles are congruent, which means that angle 1 is equal in measure to angle 2, and angle 3 is equal to angle 4.
Diagram 2: Corresponding Angles
In this diagram, we explore corresponding angles:
Explanation:
- In Diagram 2, Line l and Line m are parallel lines, cut by transversal Line t.
- The angles labeled 1 and 3 are corresponding angles, and the angles labeled 2 and 4 are also corresponding angles.
- Corresponding angles are congruent, which means that angle 1 is equal in measure to angle 3, and angle 2 is equal to angle 4.
Diagram 3: Alternate Interior Angles
We will now examine alternate interior angles in Diagram 3:
Explanation:
- In Diagram 3, Line l and Line m are parallel lines, cut by transversal Line t.
- The angles labeled 1 and 3 are alternate interior angles, and the angles labeled 2 and 4 are also alternate interior angles.
- Alternate interior angles are congruent, which means that angle 1 is equal in measure to angle 3, and angle 2 is equal to angle 4.
Diagram 4: Alternate Exterior Angles
Lastly, we explore alternate exterior angles in Diagram 4:
Explanation:
- In Diagram 4, Line l and Line m are parallel lines, cut by transversal Line t.
- The angles labeled 1 and 2 are alternate exterior angles, and the angles labeled 3 and 4 are also alternate exterior angles.
- Alternate exterior angles are congruent, which means that angle 1 is equal in measure to angle 2, and angle 3 is equal to angle 4.
Applications of Parallel Lines and Transversals:
Understanding parallel lines and transversals is not just an academic exercise. It has practical applications in various fields:
- Architecture: Architects use principles of parallel lines and transversals when designing buildings, ensuring that lines are parallel for structural integrity.
- Engineering: Engineers consider these principles when designing roads, railways, and other transportation infrastructure to ensure that tracks and roads remain parallel.
- Art and Design: Artists and designers often employ geometric principles to create aesthetically pleasing compositions, and knowledge of parallel lines and angles can be essential in this process.
- Navigation: Understanding parallel lines and transversals can also be vital for navigation systems and map-making.
- Real Estate: In real estate, knowledge of these concepts can help in designing property boundaries, ensuring parallel lines where necessary.
In conclusion, parallel lines cut by a transversal form the basis of various geometric concepts, helping us understand the relationships between angles and lines. The applications of this knowledge are widespread, affecting fields from mathematics and science to architecture and design. By mastering these concepts, we can gain a deeper understanding of the world around us and apply them to solve real-world problems.